|
>
intersculpt 2007
SCULPTURE ET MATHÉMATIQUES
SCULPTURE
AND MATHEMATICS
|

Philippe
CHARBONNEAU |
 |
 |
 |
 |
Le
double DVD de l'exposition et des conférences "Sculpture et
Mathématiques" est disponible à la vente au prix
de 15
euros, frais de
port inclus.
Commande
par chèque à l'ordre d'ARS MATHEMATICA, 1 cour de
Rohan, 75006 Paris, France.
The
double DVD of the exhibition and conference "Sculpture and Mathematics"
is available for sale. Price: 25 USD, shipping cost
included.
Order by cheque to ARS MATHEMATICA, 1 cour de Rohan, 75006 Paris,
France.
|
L’exposition
SCULPTURE ET MATHÉMATIQUES a été
lancée
lors de la Fête de la Science 2006 en Lorraine, accueillie
à l'AIP
PRIMECA de Nancy (campus de l'UHP).
Puis elle fut présentée sous forme de
conférence à l'Université de
Catania (Sicile), en octobre 2006, à l'invitation
du Pr. Salvatore MUSUMECI.
Cette exposition et conférence itinérante propose
d'une part un bref historique du sujet, et d’autre
part une série d’œuvres
récentes, soit sous forme d’images et
d’animations informatiques, soit sous forme
d’œuvres physiquement
matérialisées.
Une vingtaine d'artistes internationaux sont choisis,
mathématiciens de formation, ou bien sculpteurs plus
traditionnels, inspirés par les mathématiques.
A
chacune des étapes de l’exposition, des artistes
et mathématiciens sont invités à
s’exprimer devant le public, de visu et/ou par
visioconférence. Par ailleurs, l’exposition est
relayée sur Internet.
En
octobre, pour la Fête de la Science 2007, c'est la
prestigieuse ENSAM de Paris qui recevra
l'exposition et conférence SCULPTURE ET
MATHÉMATIQUES. A cette
occasion un catalogue sera publié.
Les moyens de l'ENSAM, associé à ceux de la
société AXIATEC, permettront de
réaliser des
démonstrations publiques de réalité
virtuelle en
relief, et des impressions 3D sur machine Zcorp.
dans
le cadre d'INTERSCULPT 2007
|
organisation
SÉLECTION
DES OEUVRES / CURATOR
Christian
LAVIGNE
COMITE
SCIENTIFIQUE
Monique
BLANC
Simon DINER
Nicolas
HUEBER
Marc
LACHIEZE-REY
COORDINATEURS
Patrick
COLLANDRE
Patrick
SAINT-JEAN
RELATIONS
PUBLIQUES
Aude BLANC-BRUDE
LIEU
/ PLACE
ENSAM
(Ecole Nationale Supérieure des Arts et Métiers),
151 Bd de l'Hôpital, 75013 Paris, France.
DATES
EXPOSITION / EXHIBITION DATES:
Mercredi 10
- Mercredi 17 octobre 2007.
Wednesday
10 to Wednesday 17 of October, 2007.
HEURES
DOUVERTURE / OPENING HOURS:
12H-19H
DATE
CONFÉRENCE :
Samedi 13
octobre 2007.
Saturday
13, October, 2007.
10H30-19H30
ARTISTES
CONCERNÉ
CONCERNED ARTISTS:
Tous les sculpteurs
inspirés par les mathématiques / All sculptors
using maths in their works.
CONFÉRENCIERS
/ SPEAKERS:
Artistes /
Artists
Mathématiciens / Mathematicians
Critiques d'art / Art critics
Ingénieurs
/ Engineers
|
The
SCULPTURE AND MATHEMATICS exhibition was first launched during the
Fête de la Science 2006 in Lorraine, welcomed at the AIP
PRIMECA Lab in Nancy (Université Henri
Poincaré).
Then it was presented as a lecture at the University of Catania
(Sicilia), in October 2006, thanks to the Pr. Salvatore
MUSUMECI.
The
SCULPTURE AND MATHEMATICS Exhibition tells the story of the theme and
shows a number of recent works, either computer images and animations
or pieces physically materialized.
About
20
international artists are choosen, who had academic trainings
in
mathematics, or who are more traditional sculptors -
inspired
by maths.
At each event venue, artists and
mathematicians will express themselves, either in person or
by videoconferencings. The exhibition and the lectures will be
displayed on the Web.
This
year, in October 2007, during the "Fête de la Science", it's
the very prestigious École
Nationale Supérieur des Arts et Métiers
de Paris which will welcome the exhibition and conference SCULPTURE AND
MATHEMATICS. A bilingual catalogue (French-English)
will be published.
The
ENSAM and AXIATEC (Zcorp and Sensable representative in
France)
means and equipments will allow us to make public live demonstrations,
in terms of Virtual Reality and Rapid Prototyping.
|
objectifs
généraux
- Montrer
que l'art et la science font parti d'une même culture.
- Présenter
les perspectives nouvelles de recherche et de
création offertes par l'informatique, les réseaux
et les
"Technologies de l'Objet Numérique".
- Faire
œuvre de pédagogie à la fois
vis-à-vis du grand public et des chercheurs et scientifiques.
- Susciter
des partenariats nouveaux entre artistes et chercheurs.
|

Stewart
DICKSON |
main
purposes
- To
show that art and science are parts of a same culture.
- To
present the new perspective for research and creation offered by
computing, the Web and the 'Technologies of the Digital Object'.
- To
inform the general public and the scientists.
- To
create new partnerships between artists and researchers.
|
|
 |
IS2007 est
relayé par le
Krannert Art Museum
et
l'Integrated
Systems Laboratory
du Beckman Institute for advanced science and technology
de
l'University of
Illinois,
Urbana-Champaign, USA. |

 |
|




|
partenaires
et sponsors
partnership
and sponsoring

|


 |
|

Patrick
COLLANDRE |
the lecturers registration to
/ l'inscription
des conférenciers à
IS2007 / SCULPT
AND MATHS
is
closed / est terminée.
PARTICIPER
A L'ÉVÉNEMENT
TO
CONTRIBUTE TO THE EVENT
merci
d'envoyer un email à C. LAVIGNE
thanks
for sending an email to C. LAVIGNE
lavigne@intersculpt.org
avec
les renseignements suivants
with
the following informations:
1. prénom, nom, adresse postale / first name, last name,
postal address
2. adresse email, site Web / email address, Web site
3. résumé biographique / short biography
4. images jpg ou gif d'oeuvres proposées / jpg or gif
pictures of the proposed works
ensuite,
pour le site Web de l'expo, pour les affiches et les écrans
de
présentation des artistes, le catalogue de l'exposition, la
production éventuelle d'oeuvres in situ (nous disposerons
d'une
Zcorp), il sera nécessaire d'envoyer via un FTP...
then,
for
the exhibition Web pages, the posters and the screens that will present
the artists works, the pieces we may build in the exhibition
(we
will have a Zcorp at our disposal), it will be necessary to
send via a FTP...
1. des images haute résolution
2. et/ou des fichiers VRML
3. et/ou des fichiers STL
DATE
LIMITE / DEADLINE
30
JUIN 2007 / 30, JUNE 2007
|

Alexandre
VITKINE |

Bathsheba
GROSSMAN |
les
artistes de
Sculpture et Mathématiques 2007
/
the Sculpture and Mathematics 2007
artists
|
Raymond
ASCHHEIM |

Salvatore
MUSUMECI |

Eddy PARKIET |

George W.
HART |
artistes
présentés / presented artists
- Raymond
ASCHHEIM (France)
- Mary
BATES-NEUBAUER (USA)
- Philiipe
CHARBONNEAU (France)
- Jonathan
CHERTOK (USA)
- Patrick
COLLANDRE (France)
- Stewart
DICKSON (USA)
- Helaman
FERGUSON (USA)
- Herbert
W. FRANKE (Allemagne)
- Gregorio
FRANZONI (Italie)
- Pierre
GALLAIS (France)
- Bathsheba
GROSSMAN (USA)
- Michael
HANSMEYER (UK)
- George
W. HART (USA)
- Paul
HIGHAM (USA)
- Peter
JANSEN (Hollande)
|
- Christian
LAVIGNE (France)
- Salvatore
MUSUMECI (Italie)
- Eddy
PARKIET (France)
- Sylvie
PIC (France)
- Philippe
RIPS (France)
- Rinus
ROELOFS (Hollande)
- Patrick
SAINT-JEAN (France)
- SENOCOSME
(France)
- Carlo
SEQUIN (USA)
- Michael
SHAW (UK)
- David
SPRINGETT (UK)
- Simon
THOMAS (UK)
- Alexandre
VITKINE (France)
- Norwood
VIVIANO (USA)
- Derrick
WOODHAM (USA)
|
conférenciers
/ speakers
- Raymond
ASCHHEIM (POLYTOPICS, France)
- Pr.
Mary BATES-NEUBAUER (ASU, USA)
- Pr.
Monique BLANC (ENSAM, France)
- Philippe
CHARBONNEAU (France)
- Patrick
COLLANDRE (France)
- Michel
DARONAT (AXIATEC, France)
- Stewart
DICKSON (Beckman Institute, U. of Illinois, USA)
- Dr.
Simon DINER (CNRS, France)
- Dr. Gregorio FRANZONI
(Italie)
- Peter
JANSEN (Hollande)
- Sylvestre
NUNES (AFPR, France)
- Philippe
RIPS (France)
- Rinus
ROELOFS (Hollande)
- Patrick
SAINT-JEAN (ENS, France)
- Dr.
Michael
SHAW (UK)
- Stéphane
TROIS CARRÉS (France)
- Alexandre
VITKINE (France)
|
LES
PHOTOS DE L'EXPOSITION / PHOTOS OF THE EXHIBITION
 |
SAMEDI
13 OCTOBRE |
CONFERENCIER
/ SPEAKER |
PHOTO
ou/or ILLUSTRATION |
TITRE & RESUME / TITLE
AND ABSTRACT |
| 10H30-11H00 |
Patrick
SAINT-JEAN
artiste
plasticien,
enseignant-chercheur
à l'ENS Cachan, France |

|
"Le projet
PolyAgogic CyberSpace"
Le
PolyAgogic CyberSpace est le percept-concept-affect d'un
amphithéâtre interactif à immersion
pour la sculpture de la connaissance par le Design du concept
multimédia. La scénographie place les
spectateurs, spect-acteurs, interacteurs et acteurs de la connaissance
dans un espace-temps, concret-abstrait-virtuel, d'une
tétralogie des arts, sciences, technologies et philosophies,
multi, pluri et polymédia.
Numérisée, captée,
analysée, structurée, abstraite, et
virtualisée en temps réel à partir de
la toile numérique, la connaissance remplit l'espace
(knowledge mater). Puis visualisée sur plusieurs
écrans, synthétisée,
architecturée, texturée, elle est
sculptée soit systémiquement par les
texturologies quantiques et des moteurs d'intelligence, de conscience
et de vie artificielles, soit interactivement dans une humanologie
participative (intelligence collective à base d'intelligence
personnelle, collaborative et coopérative), où
les intervenants actifs et passifs créent ou inhibent les
liens du réseau dynamique pondéré,
travaillant ainsi la forme signifiante par effet de pleins et de vides
colorés et ombragés.
Scénarisée dans une mise en partition
multi-piste, la sculpture, comme nouvelle écriture, se forme
dans sa micro (quanta informationnel), mezzo (liens intimes entre
percepts-concepts-affects matérialisés dans
l'espace par des diodes laser montrant le polytope des points de vue)
et macro composition (process temps réel) sculptant ainsi
dynamiquement la matière de la connaissance et de
l'ignorance.
Ce travail est la convergence actuelle en hommage à ceux de
Iannis Xenakis, Nicola Schöffer, Nicolas Bourbaki, Gilles
Deleuze et Felix Guattari, Jean Dubuffet, René
Passeron, Michel de Certeau, Jacques Derrida, et tous ceux qui peuplent
notre culture sans qui nous ne pourrions nous sculpter. |
| 11H00-11H20 |
Philippe RIPS
sculpteur, France |
 |
"Tensegrity et
constructions légères" |
| 11H20-11H50 |
Raymond ASCHHEIM
ingénieur,
mathématicien et artiste plasticien, France |

|
"Quattuor
Quaternionibus"
De
Dali aux nombres a` 16 dimensions, un parcours
éclairé
par les mathématiques et illustré par les
premie`res
hypersculptures vous réve`lera des clefs de mythes anciens
(gene`se, cabale, alchimie, apocalypse) et de théories
scientifiques actuelles (géométrie non
commutative,
théorie des cordes, physique digitale, syste`mes complexes).
De
passionnantes questions philosophiques, métaphysiques et
scientifiques sont abordées par le langage de
l’art
visuel, plastique, dynamique et interactif.
|
| 11H50-12H10 |
Philippe CHARBONNEAU
sculpteur,
France |
 |
"Sculpture
et surfaces réglées"
|
| 12H10-12H30 |
Stéphane
TROIS CARRÉS
artiste plasticien et enseignant,
France |
 |
"Les théories
mathématiques
sont une matière plastique"
Les
mathématiques sont élaborées dans un
protocole
rationnel garantissant les résultats, mais il peut y avoir
aussi
une lecture décalée des mathématiques
qui permet
de renouveler les paradigmes esthétiques.
Ce processus ne se préoccupe pas du protocole de
validation. Sa seule horizon c'est l'imagination.
L'idéal platonicien s'est effondré avec
l'apparition
d'une multiplicité des esthétiques. Les
mathématiques devenant ainsi un processus d'exploration des
réalités possibles. Partageant ainsi son champ
d'exploration avec la littérature et la philosophie.
L'unité classique, l'effondrement post-moderne
sont balayés par la diversité des mondes.
|
| 12H30-14H00 |
PAUSE
/ BREAK |
|
|
| 14H00-14H30 |
Monique
BLANC
professeur agrégée de mathématiques,
ENSAM de Paris, France |
 |
"Exemples d’utilisation de la
CAO au CER-Paris de l’ENSAM"
La CAO s’est
imposée à l’ENSAM
à partie de l’année
1985 et sa première utilisation a été,
bien sûr, une application industrielle.
A partir de 1990 nous l’avons utilisée pour
des reconstructions virtuelles (L’église abbatiale
Cluny III par exemple).
A ce jour la CAO est
couplée au
prototypage rapide pour la réalisation d’objets et à l’immersion virtuelle.
|
| 14H30-15H00 |
Dr. Gregorio FRANZONI
responsable
R&D pour un cabinet d'architecture, en liaison avec
l'université de Cagliari, Sardaigne, Italie
|
 |
"Material models of surfaces: a
bird’s eye view from galileo’s age to rapid
prototyping"
In
the last
20 years, mathematical objects have been represented, visualized and
animated in very effective ways. Computer graphics turned out to be a
powerful tool to improve understanding of Geometry of curves and
surfaces and to attract people to Mathematics. Physical modeling of
geometric shapes can be seen as a natural extension of virtual
modeling: material models enhance our spatial perception of those
objects by adding the tactile experience to the visual one. Moreover,
in several occasions visual and material representations of
mathematical objects played a central role in research development. In
parallel with an overview of some famous models since the times of
Galileo Galilei until today, I will show some models realized by means
of several techniques and materials: plaster, wires, paper, metal and
3D printing, a technique used in manufacturing field to realize,
through a layer-by-layer constructive method, accurate physical
prototypes from 3D computer-generated models. 3D printing is probably
the most powerful tool to produce very precise models of surfaces. In
order to do that, one has to represent surfaces as solid bodies and
this can be done in a natural way by constructing a thin solid shell
around them. Such operation can be done by means of some standard
differential geometry as long as the original surface is regular and
injectively immersed in 3-space, while it requires some deeper work if
it has self-intersections or singularities. |
| 15H00-15H20 |
Patrick COLLANDRE
artiste
plasticien, France |
 |
"un TAO
platonicien"
Oui
et non (mais,
c'est déjà la dualité ). Aussi mes
axes de
recherches sont actuellement situés entre la
modélisation
des volumes et leur complémentarité, le plein et
le vide,
l’avoir et le manque, etc... un travail
d’équilibriste, quoi!. Je ne suis pas
mathématicien, mais un grand rêveur
touché par la
beauté des volumes mathématiques. Par le
passé,
j’ai illustré en 2 dimensions des paysages
imaginaires. De
grands espaces dans lesquels flottaient des sphères
constituées de 2 éléments en recherche
d’égalité de rapport. Il y a quelques
années, j’ai mis ce concept ( qui ressemble
à la
représentation du Tao ), en volume. Deux pièces
identiques, qui assemblées forment une sphère.
Ensuite,
en recherche de compréhension, je me suis frotté
à
la quadrature volumique des polyèdres platoniciens et leur
représentation de la complexité croissante. Mais
en
dehors des mots, je suis fasciné par leur beauté
simple.
Je compte sur ces volumes pour nous suggérer leur essence.
"A platonic Tao"
Yes
and no (but this is already duality).
My main research lines are at the moment inbetween the modelling of
volumes and their complementarity, plenums and vacuums, “gets
and
lacks”, etc... Such an acrobatic work!
I am not a mathematician, but a dreamer touched by the beauty of the
mathematic volumes.
In the past, I illustrated some fictional landscapes in two dimensions
— wide spaces into which spheres made of two elements in
search
of an equality ratio were floating.
Few years ago, I put this concept in volume (which looks like a Tao
representation): two identical pieces, which look like a sphere, once
put together.
Later on, looking for better understanding, I took on the quadrature
density of the platonic polyhedrons and their growing complexity.
But, besides the words, I am fascinated by their simple beauty.
I count on these volumes to give us an idea of their essence.
|
| 15H20-15H50 |
Peter JANSEN
sculpteur,
Hollande |
 |
"Strange
Attractors"
From
traditional craftsmanship I went over the last two years
to the computer as my “main
workspace”,computer-video-animation, sculpting.
I was strangely attracted to the beautiful renderings with Chaoscope of
3d strange attractors and fractals.
When I read on the forum it wouldn't be possible to make them as real
life forms I got enormously triggered.
So after a lot of exercising with an experimental version of Chaoscope
it was possible to make the right pointcloud data. By reverse
engineering I could make almost perfect meshes from he pointcloud.
After that I could make solids out of it and repair the .stl files so
they could be printed in polyamide and alumide (sls) and wit a
3dprinter in raisin for bronscasting.
|
| 15H50-16H20 |
Simon DINER
physicien
et philosophe, ancien Directeur de Recherche au CNRS, France |
 |
"La question du
nombre d'or"
le
nombre d'or
est un nombre irrationnel aux remarquables proprietes mathematiques,
que l'on a voulu a tort a partir du xix° siecle impliquer dans
des
considerations esthetiques. |
| 16h20-16H30 |
PAUSE / BREAK |
|
|
| 16H30-17H00 |
Stewart DICKSON
artiste
et chercheur au Beckman Institute de l'Université d'llinois |
 |
"Vedic Geometry
and Tactile Mathematics"
|
| 17H00-17H20 |
Hsin Hsin LIN
[videoconference]
artiste
multimédia, Singapour |
 |
"The Art of
Equations"
From
the
soft-edged apple peels to the bird of paradise and leaves, from the
hard-edged durians to desert cactus and coccothrinax, all can be
formulated entirely by a 3-equations foundation. That is, one equation
for each axis (x, y, z). The software auto computes the coordinates for
each of the x, y and z axes as well as a varying real-time driven
surface color and lighting parameters. Beyond asteroids, cardioid,
deltoids,
ellipsoids, lemniscate of Bernoulli or Gernoro, equations can be shaped
to generate nature-like
plants,
birds and
bees, marine creatures and 3D objects. Beyond the conceivable
Nautilidaes and turritellidaes, equations can be used to formulate
Balinese face masks, kimono and obi belts. These generated 3D
structures can be animated and morphed automatically, and it can be
Web-enabled.
When
creating
surfaces for the same object, equations are preferred over 3D modeling
as it is extremely scalable and it is implemented with lean
computational resources in hardware, software and manware, in fact, it
is the minimum. This economy of expression is also the most flexible in
real-time driven continuous facade changing for 3D geometry. It is an
ecological purification of mathematically generated bit streams. This
paper presents the results of an array of 3D structures formulated by
equations. |
| 17H20-17H40 |
Michel DARONAT
ingénieur,
sté AXIATEC, France |
 |
"L'impression 3D
au service de l'art, de l'architecture et du design" |
| 17H40-18H10 |
Dr. Michael SHAW
sculpteur,
GB |
|
"Rapid
prototyping Specific Objects: the sculptural
aesthetics of mathematical proportions"
The
paper will explore recent research that attempts to exploit the
sculptural potential of rapid prototyping in extending Donald
Judd's
concept Specific Objects. This has been achieved through a combination
of deflected geometry, concentric deviance, and transparent structures.
Consideration will also be given to the role of basic mathematical
phenomena as an aesthetic tool that underpins the extension of singular
forms with both variation and unity. |
| 18H40-19H00 |
Ariane GENTY
Dr
Jean-François BONNET
Maria VALLEJO HERNANDEZ
INOLAM,
France
|


 |
"ASTRALE un
projet au service de la valorisation du patrimoine"
Projet
ASTRALE
(Art Science Technologie Recherche en Amérique Latine et
Europe)
Réseau de collaborations scientifiques et culturelle France
Amérique Latine avec pour thèmes principaux :
- Établir
des relations de collaboration scientifiques et éducatives
autour de projet concernant le patrimoine, en particulier, entre les
mondes européen et latino-américain . Les
domaines
d'études envisagés concernent les sciences
liées
aux couleurs des matériaux, et les sciences du patrimoine,
(chimie/physique, optique, restauration, histoire de l'art,
archéologie, informatique et multimédia).
- Développer
des outils 3D pour la valorisation du patrimoine (musées,
collections publiques ou privées...). Avec deux axes
principaux :
1-
Le «musée virtuel 3D» ou les
«expositions
virtuelles 3D» permettant de réunir dans un
même
espace virtuels des oeuvres numérisées de
provenance
diverses (réserves de musées, collections
particulières ...).
2-
La simulation
physico-chimique des matériaux constituant une oeuvre, par
l'utilisation d'un moteur de rendu spectral basé sur les
caractéristiques physico-chimiques des matériaux.
- Se
baser principalement sur des outils libres et open source.
|
| 19H20-19H30 |
Alexandre VITKINE
infosculpteur |
 |
"Comment
obtenir des infosculptures simples et comment
définir la simplicité ?"
Mes sculptures ou gravures sont
simples - c'est ce que j'aime.
L'utilisation
des mathématiques permet de créer des formes
simples.
Comment
définir la simplicité:
Le grand
spécialiste de la simplicité au MIT, John MAEDA,
déclare:
"Simplicity
and complexity need each other."
C'est
à dire: Cette entité exige l’existence
de son contraire.
J'ai
défini la
simplicité comme l'inverse de la complexité ,ce
qui
donne:
sim = 1/com ou ksim = 1000/com
Comment
chiffrer la complexité:
Compter le
nombre d'éléments de l'œuvre : Symbole
com.
Comment
définir un élément:
C'est une
ligne ou une surface plane ou gauche sans discontinuité.
(Un volume
est défini par la surface qui l'entoure)
Quelques
exemples:
Sphère
com=1 ksim = 1000
Hémisphère
com=2 ksim = 500
Cube
com=6 ksim = 167
_________
Tout cela
peut être contesté:
Si nous
voyons la surface
de la sphère comme composée d'une
infinité de
surfaces élémentaires, nous obtenons:
com =
infini ksim = 0
---------------
Que
pensez-vous de tout cela ? |
| 19h30-19H45 |
questions du
public
conclusions |
|
|
|
|

Rinus
ROELOFS |

Mary BATES
NEUBAUER |

Carlo SEQUIN |
|
|
SCULPTURE ET MATHEMATIQUES
une
brève introduction , par Christian LAVIGNE.
Depuis
des millénaires, la sculpture et l'architecture sont
intimement
liées à la géométrie et aux
mathématiques.
L'art
comme la science ont pour ambition de
donner une description de l'univers, et les premiers textes que nous
connaissons à propos d'une vision
géométrique de
l'espace remontent aux Grecs.
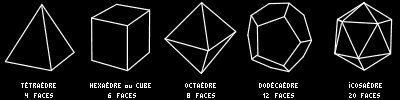
Ceux-ci
avaient étudié entre autres les fameux 5
polyèdres réguliers, dits solides platoniciens :
Ils
connaissaient aussi la sphère, le cylindre, le
cône, le
tore, l'hélice, etc. Ces figures étaient
abondamment
utilisées dans l'architecture depuis la plus haute
Antiquité. Pour ce qui est de la sculpture, même
la plus
figurative, elle empruntait aux mathématiques la science des
nombres et des proportions.
Dans
l'art européen "moderne" , qui émerge
après mille
ans de Moyen-Age, c'est à dire l'art qui se crée
à
partir de la Renaissance, l'intérêt pour les
figures
géométriques se renouvelle et s'amplifie
grâce
d'une part à l'évolution des recherches
mathématiques, et d'autre part aux outils (intellectuels et
concrets) de la perspective.
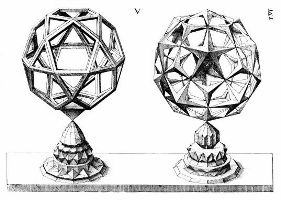
polyèdres
de VINCI et
de JAMNITZER
Au
XVIIe siècle, l'invention de la
géométrie
algébrique (c'est à dire la description des
points de
l'espace par leurs coordonnées dans un repère que
l'on se
fixe) par René DESCARTES, ouvre des horizons nouveaux et
considérables, à la fois pour les
démonstrations
mathématiques et pour la création de formes
d'après des équations.
Après
les travaux d'EULER au XVIIIe siècle, c'est surtout au XIXe
siècle que se développent les grandes
théories
géométriques, grâces aux recherches de
PONCELET,
MONGE, MÖBIUS, KLEIN…Et consécutivement
la
découverte de nombreuses figures mathématiques du
plan et
de l'espace. Á partir de 1860 on commence à
créer,
d'abord en Allemagne, des modèles en plâtre et en
fil de
fer de ces courbes et surfaces, dont la vogue s'étend aux
universités européennes et
américaines, puis
disparaît au début du XXe siècle.
 
C'est
justement à cette période que naissent le cubisme
et
l'art abstrait. Le CONSTRUCTIVISME en particulier
s'intéresse de
près aux relations entre art et science. Les sculptures de
Naum
GABO montrent une influence nette des objets mathématiques.
Certaines œuvres d'artistes comme Anton PEVSNER, Man RAY,
Henry
MOORE, Max BILL, Barbara HEPWORTH … se
réfèrent
explicitement à des modèles
géométriques.
Man RAY a d'ailleurs expliqué, dans un livre de souvenirs,
comment il avait été invité par son
ami Max ERNST,
au milieu des années 30, à découvrir
les
collections de plâtre de l'Institut Henri
Poincaré,
où il est resté plusieurs jours à
prendre des
photos. Il peindra ensuite une série intitulée
Shakespearean Equations.
 
Man RAY
Le
mouvement de l'art abstrait géométrique perdure
jusqu'à nos jours, mais d'une manière
générale les figures mathématiques
utilisées sont restées simples, les artistes
jouant
plutôt sur la répétition, la
symétrie ou la
dissymétrie, le rythme, la couleur, les effets
optiques…Il existe aussi ce qu'on pourrait appeler un "art
figuratif géométrique", magistralement
illustré
par M.C. ESCHER.
L'avènement
de la micro-informatique donna un nouvel essor aux recherches et
visualisations géométriques. La
découverte de
nouvelles surfaces minimales, la théorie des fractales,
produisirent des images inédites qui inspireront des travaux
artistiques. D'autres approches (le chaos, les écoulements
fluides, les automates cellulaires, etc.) donneront lieu à
des
créations 2D fixes ou évolutives.
Pour
ce qui concerne l'art du volume, c'est le mouvement de la sculpture
numérique, né véritablement au
début des
années 80, après les expériences
isolées de
Pierre BÉZIER ou de Georg NEES, qui revivifie l'abstraction
géométrique, en utilisant à la fois
les ressources
de l'informatique pour la visualisation des formes, et celles de la
robotique pour leur matérialisation physique (machines
à
commande numérique, gravure laser et impression 3D).
Bien
des artistes d'INTERSCULPT, biennale mondiale de sculpture
numérique lancée par l'association
française Ars
Mathématica (fondée par A. VITKINE et C.
LAVIGNE),
s'inspirent directement des mathématiques. L'un des premiers
d'entre eux fut l'américain Stewart DICKSON, qui produisit
en
Stéréolithographie des surfaces minimales au tout
début des années 90.
Plus
récemment, un autre américain, architecte de
formation,
Jonathan CHERTOK, entreprit de remodéliser en 3D l'ensemble
des
surfaces inventoriées et fabriquées
artisanalement depuis
le XIXe siècle, tandis que le français Patrice
JEENER
réalise lui des gravures sur cuivre de ces
modèles, et de
nouvelles figures explorant les dimensions supérieures
à
3.
Les sculpteurs séduits par les objets
mathématiques sont
de formation très diverses: certains d'entre eux sont
à
la base des mathématiciens professionnels, des
ingénieurs, des universitaires; d'autres
viennent des
cursus habituels des Beaux-Arts.
De
même, les techniques et les matériaux sont
variés:
- fraisage
numérique
- gravure
3D au laser dans des blocs de cristal
- prototypage/fabrication
rapide, impression 3D
- fonte
d'aluminium, de bronze ou de métaux précieux
- techniques
traditionnelles de la sculpture...
Dans
la plupart des cas, lorsque la maquette ou bien le fichier informatique
de l'œuvre
mathématique a été
créé, on peut
choisir ensuite les dimensions et l'aspect du résultat
final,
c'est à dire que l'on peut aussi bien produire des petits
bijoux
en or que des pièces en bronze, ou des sculptures
monumentales
en marbre. La singularité de l’art
mathématique est
de ne pas avoir d’échelle, c’est
à dire
qu’il est impossible de savoir devant l’image ou la
photographie d’une oeuvre quelle est la taille de celle-ci !
Les
œuvres que nous présentons dans
l'exposition ne nous donnent qu'un
aperçu des travaux actuels des sculpteurs
inspirés par la
géométrie et les mathématiques:
l'exploration des
formes et des univers continue ! |
SCULPTURE AND MATHEMATICS
a
short introduction, by Christian LAVIGNE.
Since
thousands of years, sculpture and architecture are intimately linked to
geometry and mathematics. Art and science intend both to describe the
world, and the first texts of a geometric vision of space are
Greek.
The
Greek had, among others, studied the famous 5 regular polyhedrons, the
so called Platonic solids.
They
knew also the sphere, the cylinder, the cone, the torus, the helix etc.
These figures were copiously used in architecture since the earliest
times. Even very figurative sculptures used the mathematical laws of
numbers and proportions.
In
the "modern" European art ( after the Middle Ages, during which the
Arab civilization used geometry for aesthetic purposes ) i.e. from the
Renaissance onward, the interest for geometric figures increases. This
thanks to mathematical research and the intellectual and material tools
for the perspective.
In
the 17th century, the invention of analytical geometry ( points of
space defined by their coordinates) by René DESCARTES, opens
new
horizons for the creation of shapes from equations.
After
EULER in the 18th century, the great geometrical theories
emerge
during the 19th century thanks to PONCELET, MONGE, MÖBIUS,
KLEIN… Consecutively, numerous new mathematical figures
are discovered. Between 1860 and the end of the
century,
models in plaster or wire were created first in Germany, then in
European and American universities.
At
the same time, Cubism and Abstract Art were born. CONSTRUCTIVISM was
particularly interested in the relation between art and science. The
works of Naum GABO show a marked influence of mathematical
objects. Certain works of artists such as Anton PEVSNER, Man
RAY,
Henry MOORE, Max BILL, Barbara HEPWORTH … refer clearly to
geometric models. Man RAY recalls how his friend Max ERNST made him
discover the plaster models of the Henri Poincaré Institute,
in Paris. He
took pictures and then painted a series which he called Shakespearean
Equations.
The
movement Abstract Art continues until now but the mathematical figures
in use remain simple, the artist using repetition, symmetry and
asymmetry, rhythm, colour, optical effects…A
"figurative
geometric art" also exists, brilliantly illustrated by M. C. ESCHER.
With
the arrival of the micro-computer and the discovery of new minimal
surfaces and the fractals, new images could inspire the artist. Other
approaches (the chaos, flow of liquids, cellular robots etc.) have
produced fixed or changing 2D creations.
Computer
sculpture started in the early eighties, after some experiments of
Pierre BEZIER and Georg NEES: display of 3D forms on the computer
screen, materialized by robotics.
Mathematics
has inspired the artists who participate in INTERSCULPT, the
biennial launched by the French association ARS MATHEMATICA (founded by
A. VITKINE and C. LAVIGNE).
One
of the first participants was the American Stewart DICKSON
who
produced minimal surfaces through Stereolithography in the early 90.
More recently, another American, Jonathan CHERTOK, architect, started
producing all the mathematical surfaces which had been hand-made since
the 19th century, and a Frenchman, Patrice JEENER, made
copperplate
etchings which explored more than 3 dimensions.
The sculptors interested by mathematical shapes have very different
backgrounds: the ones are professionals mathematicians, engineers,
academics; the others come from usual Fine Arts trainings.
The
crafts used are various too:
- Computer
controlled milling
- Laser
3D engraving in crystal blocs.
- Rapid
prototyping, 3D printing
- Casting
of aluminium, bronze or precious metals
- Traditional
sculpture techniques...
The
works we show in this exhibition are only a glimpse of to-days
geometrical or mathematical sculptures:
the
exploration continues !
|
|
|
retour
/ back |
|